Question

For a confidence level of 96%, find the critical Z-value using the Standard normal Table.

Answer 1

Assuming a two-tailed critical value, here are the steps in getting the critical value.

1. Convert the given confidence level to decimal form.

`96\%=0.96`

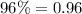
2. Divide the result by 2

`0.96/2=0.48`

3. Using the standard normal distribution table, locate the z-value that has an area of 0.48 from the center.

The z-value that has an area of 0.48 from the center is ± 2.054. Hence, the critical values are z = -2.05 and z = 2.05 for two-tails at 96% confidence level.

Assuming a one-tailed critical value, here are the steps in getting the critical value.

1. Subtract 0.5 from 0.96.

`0.96-0.5=0.46`

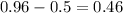
2. Locate the z-value that has an area of 0.46 to the right of the center using the Standard Normal Distribution Table.

The z-value that has an area of 0.46 to the right of the center is 1.751. Hence, the critical value for one-tailed at 96% confidence level is 1.75.

To summarize, we have: