Question

Using Euler's formula, how manyedges does a polyhedron with 4faces and 4 vertices have?[?] edgesEuler's Formula: F + V = E + 2

Answer 1

6

Step-by-step explanation:

Given;

Number of faces (F) = 4

Number of vertices (V) = 4

Number of edges (E) = ?

We can go ahead and determine the number of edges(E) of the polyhedron using the below Euler's formula by substituting the given values and solving for E;

`\begin{gathered} F+V=E+2 \\ 4+4=E+2 \\ 8=E+2 \end{gathered}`

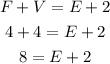
Let's subtract 2 from both sides of the equation;

`\begin{gathered} 8-2=E+2-2 \\ 6=E \\ \therefore E=6 \end{gathered}`

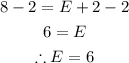
So the number of edges of the polyhedron is 6