Let's call the total amount of holiday cookies as A. The total amount of cookies is given by the product between the rate the person takes to frost the cookies by the amount of time it took to frost them. Let's call the rate Tina frost her holiday cookies as T. Since Tina takes 3 hours to frost the cookies, we have the following equation for both quantities
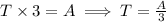
When Tina and Candy frost together, we add their rates. Let's call the rate Candy frosts as C.
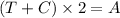
If we substitute the first expression for the T on the second expression, we have
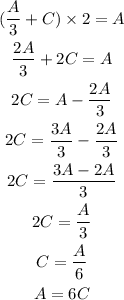
From the last expression, we have that the rate Candy takes to frost times 6 is equal to the total amount of cookies, which means that Candy takes 6 hours to frost by herself.