Question

It takes Tina 3 hours to frost her holiday cookies, but if Candy helps her it takes 2 hours. How long, in hours and minutes, would it take Candy to frost the holiday cookies by herself? Write your answer in mixed units

Answer 1

Let's call the total amount of holiday cookies as A. The total amount of cookies is given by the product between the rate the person takes to frost the cookies by the amount of time it took to frost them. Let's call the rate Tina frost her holiday cookies as T. Since Tina takes 3 hours to frost the cookies, we have the following equation for both quantities

`T*3=A\implies T=(A)/(3)`

When Tina and Candy frost together, we add their rates. Let's call the rate Candy frosts as C.

`(T+C)*2=A`

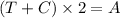
If we substitute the first expression for the T on the second expression, we have

`\begin{gathered} ((A)/(3)+C)*2=A \\ (2A)/(3)+2C=A \\ 2C=A-(2A)/(3) \\ 2C=(3A)/(3)-(2A)/(3) \\ 2C=(3A-2A)/(3) \\ 2C=(A)/(3) \\ C=(A)/(6) \\ A=6C \end{gathered}`

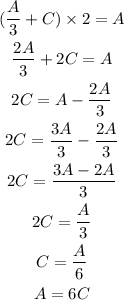
From the last expression, we have that the rate Candy takes to frost times 6 is equal to the total amount of cookies, which means that Candy takes 6 hours to frost by herself.