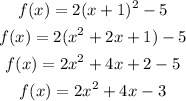We have the function:
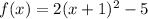
We can calculate the minimum value of f(x) looking at (x+1)^2.
This part of the function has a minimum value of 0 (when x=-1). For any other value of x, this part of the function is always higher than 0.
Then, if this is the minimum value for (x+1)^2, then the minimum value for f(x) is f(-1)=0-5=-5.
We can express f(x) as: