1. Kinetic Energy at B, C, D, and E.
To find the velocity at B, we have to use the following equation.
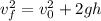
Where h = 15m, g = 10 m/s2.
![\begin{gathered} v^2_f=2\cdot10m/s^2\cdot15m \\ v^2_f=300m^2/s^2 \\ v_f=\sqrt[]{300m^2/s^2} \\ v_f\approx17.32m/s \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/bc5gtgm0aljz309qcj2gpanw2wou6azt8z.png)
Then, we find the kinetic energy at B.
![\begin{gathered} K_B=(1)/(2)m\cdot v^2=(1)/(2)\cdot1200\operatorname{kg}\cdot(17.32m/s)^2 \\ K_B=180,000J \end{gathered}]()
The kinetic energy at B is 180,000 Joules.
At C, the kinetic energy is maxed and it's equal to the potential energy at A.
![\begin{gathered} K_C=U_A=m\cdot g\cdot h_A \\ K_C=1200\operatorname{kg}\cdot10m/s^2\cdot30m \\ K_C=360,000J_{} \end{gathered}]()
The kinetic energy at C is 360,000 Joules.
At D, the kinetic energy is one-third from the potential energy at A because it's halfway.
![\begin{gathered} K_D=(1)/(3)\cdot U_A=(1)/(2)\cdot m\cdot g\cdot h_A \\ K_D=(1)/(3)\cdot1200\operatorname{kg}\cdot10m/s^2\cdot30m \\ K_D=120,000J \end{gathered}]()
The kinetic energy at D is 120,000 Joules.
At E, the kinetic energy is two-thirds of the potential energy at A.
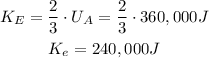
The kinetic energy at E is 240,000 Joules.
The potential at B, C, D, and E, are
![\begin{gathered} U_B=m\cdot g\cdot h_B=1200\operatorname{kg}\cdot10m/s^2\cdot15m=180,000J \\ U_C=0 \\ U_D=1200\operatorname{kg}\cdot10m/s^2\cdot10m=120,000J \\ U_E=1200\operatorname{kg}\cdot10m/s^2\cdot20m=240,000J \end{gathered}]()
The velocities at B, C, D, E are
![\begin{gathered} v_B=17.32m/s \\ K_C=(1)/(2)m\cdot v^2_C \\ 360,000J=(1)/(2)\cdot1200\operatorname{kg}\cdot v^2_C \\ v_C=\sqrt[]{600m^2/s^2} \\ v_c\approx24.5m/s \\ \\ 120,000J=(1)/(2)\cdot1200\operatorname{kg}\cdot v^2_D \\ v_D=\sqrt[]{200} \\ v_D\approx14.14m/s \\ \\ 240,000J=(1)/(2)\cdot1200\operatorname{kg}\cdot v^2_E \\ v_E=\sqrt[]{400} \\ v_e\approx20m/s \end{gathered}]()