Question

Question 57! I have no idea what the answer is would love some help

Answer 1

Question 57.

Give the following data sets:

• 0, 0, 10, 10

,

• 0, 1, 9, 10

,

• 2, 3, 5, 7

,

• 2, 4, 6, 8

,

• 5, 5, 5, 5

Let's determine the data set with the largest standard deviation.

Now, let's find the standard deviation for each data set.

• Data set A:

First find the mean

`mean=(0+0+10+10)/(4)=(20)/(4)=5`

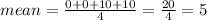
The standard deviation will be:

`\begin{gathered} s=\sqrt{((0-5)^2+(0-5)^2+(10-5)^2+(10-5)^2)/(4)} \\ \\ s=\sqrt{(100)/(4)}=√(25)=5 \end{gathered}`

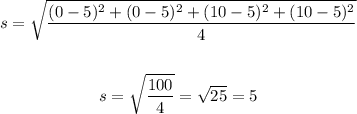
The standard deviation for data set A is 5.

• Data set B;

Let's find the mean and use the mean to find the standard deviation:

`\begin{gathered} mean=(0+1+9+10)/(4)=(20)/(4)=5 \\ \\ s=\sqrt{((0-5)^2+(1-5)^2+(9-5)^2+(10-5)^2)/(4)} \\ \\ s=\sqrt{(25+16+16+25)/(4)}=\sqrt{(82)/(4)}=√(20.5)=4.5 \end{gathered}`

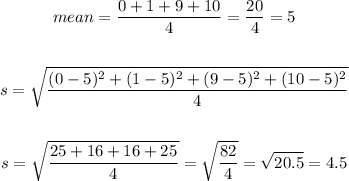
The standard deviation of set B is 4.5

• Data set C:

Let's find the mean and use the mean to find the standard deviation:

`\begin{gathered} mean=(2+3+5+7)/(4)=(17)/(4)=4.25 \\ \\ s=\sqrt{((2-4.25)^2+(3-4.25)^2+(5-4.25)^2+(7-4.25)^2)/(4)} \\ \\ s=\sqrt{(5.0625+1.5625+1.5625+7.5625)/(4)} \\ \\ s=\sqrt{(15.75)/(4)}=1.98 \end{gathered}`

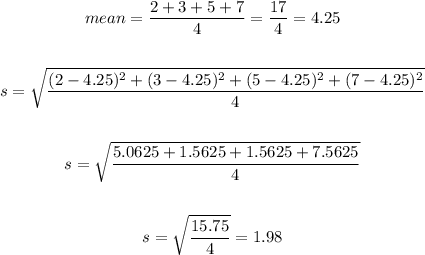
The standard deviation of data set C is 1.98

• Data set D:

`\begin{gathered} mean=(2+4+6+8)/(4)=(20)/(4)=5 \\ \\ s=\sqrt{((2-5)^2+(4-5)^2+(6-5)^2+(8-5)^2)/(4)} \\ \\ s=\sqrt{(9+1+1+9)/(4)}=\sqrt{(20)/(4)}=√(5)=2.24 \end{gathered}`

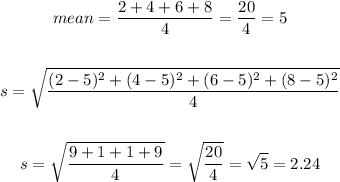
The standard deviation of data set D is 2.24.

• Data set E.

`\begin{gathered} mean=(5+5+5+5)/(4)=(20)/(4)=5 \\ \\ s=\sqrt{((5-5)^2+(5-5)^2+(5-5)^2+(5-5)^2)/(4)} \\ \\ s=\sqrt{(0)/(4)}=0 \end{gathered}`

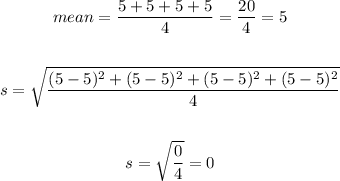
The standard deviation of data set E is 0.

Therefore, the data set that has the largest standard deviation is data set A because it has the largest standard deviation of 5.

ANSWER:

A. 0, 0, 10, 10