Question

State whether the given set of lines are parallel, perpendicular or neither.Line A has points (-1,3) and (5,1) Line B has points (-2,3) and (0,9)The lines are Answer

Answer 1

Step 1:

Line A and line B are parallel if the slope of line A is equal to the slope of line B

Line A and line B are perpendicular if the product of the slope of line A and the slope of line B is equal to - 1.

Step 2:

Line A has points (-1,3) and (5,1)



Line B has points (-2,3) and (0,9)

Next, find the slope of lines A and B

`\begin{gathered} \text{For line A} \\ x_1\text{ = -1} \\ y_1\text{ = 3} \\ x_2\text{ = 5} \\ y_2\text{ = 1} \\ \text{Slope = }(y_2-y_1)/(x_2-x_1)\text{ } \\ =\text{ }\frac{1\text{ - 3}}{5\text{ + 1}} \\ =\text{ }(-2)/(6) \\ =\text{ }(-1)/(3) \\ \text{Slope of line A = }(-1)/(3) \end{gathered}`
`\begin{gathered} \text{For line B} \\ x_1=-2,y_1\text{ = 3} \\ x_2=0,y_2\text{ = 9} \\ \text{Slope = }\frac{9\text{ - 3}}{0\text{ + 2}} \\ =\text{ }(6)/(2) \\ \text{Slope of line B = 3} \end{gathered}`

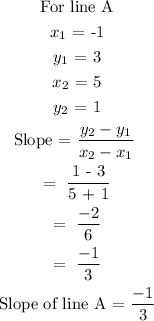
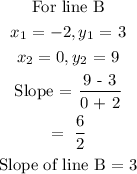
Step 3:

Line A is not parallel to line B since the slope of A is not equal to the slope of B.

`\begin{gathered} \text{Hence} \\ L\text{ine A is perpendicular to line B because } \\ \text{Slope of line A }*\text{ Slope of line B = -1} \\ (-1)/(3)\text{ }*\text{ 3 = -1} \end{gathered}`

Final answer

The lines are perpendicular.