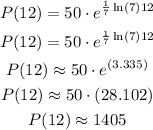According to the exponential growth model, the population at any time instant is given by,

a)
Given that the initial population is 50,

Then the function becomes,
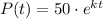
Given that after 7 years, there are 85 fish,
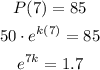
Taking logarithms on both sides,
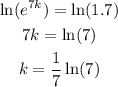
Substitute the value in the expression,
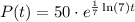
Thus, the required expression is,
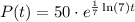
If 'y' denotes the number of fish after time 't' years, then the expression becomes,

b)
The population of fish after 12 years is calculated as,