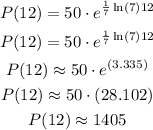Question

Writing and evaluating a function modeling continuous...An initial population of 50 fish is introduced into a lake. This fish population grows according to a continuous exponential growth model. There are 85 fish inthe lake after 7 years.

Answer 1

According to the exponential growth model, the population at any time instant is given by,

`P(t)=P_(\circ)\cdot e^(kt)`

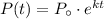
a)

Given that the initial population is 50,

`\begin{gathered} P(0)=50 \\ P_(\circ)\cdot e^(k(0))=50 \\ P_(\circ)\cdot e^((0))=50 \\ P_(\circ)(1)=50 \\ P_(\circ)=50 \end{gathered}`

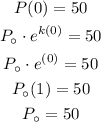
Then the function becomes,

`P(t)=50\cdot e^(kt)`

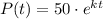
Given that after 7 years, there are 85 fish,

`\begin{gathered} P(7)=85 \\ 50\cdot e^(k(7))=85 \\ e^(7k)=1.7 \end{gathered}`

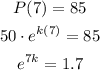
Taking logarithms on both sides,

`\begin{gathered} \ln (e^(7k))=\ln (1.7) \\ 7k=\ln (7) \\ k=(1)/(7)\ln (7) \end{gathered}`

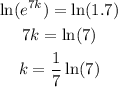
Substitute the value in the expression,

`P(t)=50\cdot e^{(1)/(7)\ln (7)t}`

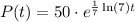
Thus, the required expression is,

`P(t)=50\cdot e^{(1)/(7)\ln (7)t}`

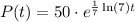
If 'y' denotes the number of fish after time 't' years, then the expression becomes,

`y=50\cdot e^{(1)/(7)\ln (7)t}`

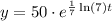
b)

The population of fish after 12 years is calculated as,

`\begin{gathered} P(12)=50\cdot e^{(1)/(7)\ln (7)12} \\ P(12)=50\cdot e^{(1)/(7)\ln (7)12} \\ P(12)\approx50\cdot e^((3.335)) \\ P(12)\approx50\cdot(28.102) \\ P(12)\approx1405 \end{gathered}`