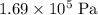Question

A horizontal pipe has varying cross-section, with one section having a diameter of 5.5cm and another section having a diameter of 4.6 cm. When a fluid of density 3.38 g-cm-3 flows through the pipe, it has a flow speed of 715 cm-s-1 and pressure of 3.45 x 105 Pa in the section with diameter 5.5 cm.A) Calculate the flow speed (in m-s-1) of the fluid in the section with diameter 4.6 cm.B) What is the pressure (in × 105 Pa) in the section with diameter 4.6 cm?

Answer 1

Given data:

* The given section with the diameter d_1 = 5.5 cm.

* The flow speed of the fluid in the section with the diameter d_1 is v_1 = 715 cm/s.

* The diameter of the other section is d_2 = 4.6 cm

* The density of the fluid is,

`d=3.38gcm^(-3)`

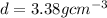
* The pressure of fluid in the section with diameter d_1 is,

`P_1=3.45*10^5\text{ Pa}`

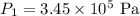
Solution:

(A). The flow rate of the fluid remains constant, thus,

`A_1v_1=A_2v_2`

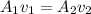
where A_1 is the area of the section with diameter d_1, A_2 is the area of the other section with diameter d_2, and v_2 is the velocity of the fluid in section with diameter d_2,

The area of the section with diameter d_1 is,

`\begin{gathered} A_1=\pi*((d_1)/(2))^2 \\ A_1=(\pi d^2_1)/(4)_{} \end{gathered}`

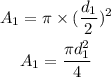
Substituting the known values,

`\begin{gathered} A_1=\frac{\pi*(5.5)^2^{}}{4} \\ A_1=23.76cm^2 \end{gathered}`

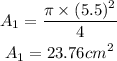
The area of the other section of pipe with diameter d_2 is,

`\begin{gathered} A_2=(\pi d^2_2)/(4) \\ A_2=(\pi*4.6^2)/(4) \\ A_2=16.62cm^2 \end{gathered}`

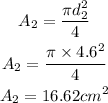
Thus, the velocity of the fluid from the other section with diameter d_2 is,

`\begin{gathered} A_1* v_1=A_2* v_2 \\ 23.76cm^2*715*10^(-2)ms^(-1)=16.62cm^2* v_2 \\ 23.76cm^2*7.15ms^(-1)=16.62cm^2* v_2 \\ v_2=(23.76*7.15)/(16.62)ms^(-1) \end{gathered}`

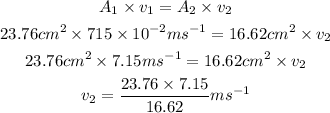
By simplifying,

`\begin{gathered} v_2=(169.9)/(16.62)ms^(-1) \\ v_2=10.22ms^(-1) \end{gathered}`

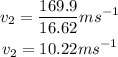
Thus, the velocity of the fluid from the other section with a diameter of 4.6 cm is 10.22 m/s.

(B). From Bernoulli's principle, the relation between the pressure and velocity on each section is,

`P_1+(1)/(2)d_{}v^2_1=P_2+(1)/(2)dv^2_2`

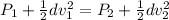
where d is the density of the fluid, P_1 is the pressure of fluid in the section with diameter d_1 and p_2 is the pressure of the fluid in the section with the diameter d_2,

Substituting the known values,

`3.45*10^5*(1)/(2)*3.38*10^{3^{}}*(715*10^(-2))^2=P_2*(1)/(2)*3.38*10^{3^{}}*(10.22)^2`

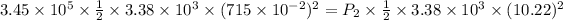
By simplifying,

`\begin{gathered} 3.45*10^5*(1)/(2)*3.38*10^{3^{}}*(7.15)^2=P_2*(1)/(2)*3.38*10^{3^{}}*(10.22)^2 \\ 298.07*10^8=P_2*176.5*10^3 \\ P_2=(298.07*10^8)/(176.5*10^3) \\ P_2=1.69*10^5\text{ Pa} \end{gathered}`

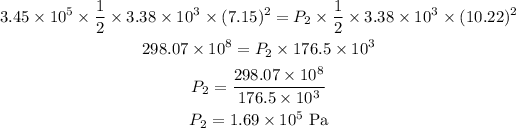
Thus, the pressure of fluid in the section with a diameter of 4.6 cm is,

`\text{1}.69*10^5\text{ Pa}`