In order to find the maximum height, we need to find the vertex of the quadratic equation.
To do so, first let's identify the parameters a, b and c from the standard form:
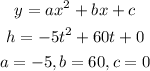
Now, we can use the formula below for the vertex x-coordinate:
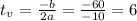
Now, calculating the vertex y-coordinate, we have:
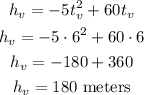
Therefore the maximum height is 180 meters.
Since the vertex occurs for a time of 6 seconds and the time of flight is double the vertex time, the flight time is 12 seconds.