Question

Which is a true statement about this triangle?20y35°cos(55)=у20sin(55)y20tan(55) ==y20O tan(55)=20y

Answer 1

Using the trigonometric functions in a right triangle,

`\begin{gathered} \cos =\frac{adjacent}{\text{hypotenuse}} \\ \tan =\frac{opposite}{\text{adjacent}} \\ \sin =\frac{opposite}{\text{hypotenuse}} \end{gathered}`

The right triangle can be resketched to get the third unknown angle;

`\begin{gathered} 90+35+\theta=180^0\text{ (sum of angles in a triangle)} \\ 125^0+\theta=180^0 \\ \theta=180-125 \\ \theta=55^0 \end{gathered}`

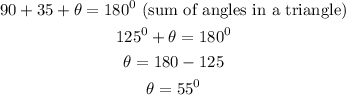
Considering angle 55 degrees as a reference,

side y is the adjacent and side 20 is the hypotenuse.

Thus, the trigonometric identity that combines adjacent and hypotenuse is cosine.

Therefore,

`\begin{gathered} \cos =\frac{\text{adjacent}}{\text{hypotenuse}} \\ \cos (55)=(y)/(20) \end{gathered}`

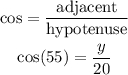
Thus, the first option is correct.