Recall that the slope-intercept form of a line is in the form
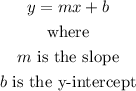
Given the equation x + 8y = 1, convert the equation to slope intercept form

Now that it is in the slope intercept form, we have determined that the slope is m = -1/8.
a.) Slope of the line that is parallel
The slope of a line parallel to the given line equation is the same slope to the line, in which case it is m = -1/8.
b.) Slope that is perpendicular to the given line
The slope of a line perpendicular to the given line is the negative reciprocal of the slope.
Solve for the negative reciprocal

Therefore, the slope perpendicular to the given line is m = 8.