Question

Please helpA sodium isotope has a half-life of 15 hours, and 500 grams are initially present. How many hours will it take the isotope to decay to 25 grams? Write and solve an exponential equation to find the answer. Round answer to nearest tenth.

Answer 1

Here, we want to write and solve an exponential equation.

The exponential equation can be written as;

`P\text{ = I }* e^(-kt)`

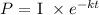
Where P represents the present mass to be calculated

I is the initial mass given

k is the radioactive decay constant

and t is the time taken to reach the present given mass.

From the question;

P = 25 grams

I = 500 grams

t = ?

k can be calculated using the equation;

k = ln 2/half-life

From the question, the half-life is given as 15 hours

Hence, l = ln 2/15

Substituting this in the decay equation, we have;

25 = 500 * e^-(ln 2/15 * t)

divide both sides by 500

0.05 = e^-(0.0462 * t)

0.05 = e^(-0.0462t)

Find the ln of both sides

ln 0.05 = ln e^(-0.0462t)

-2.996 = -0.0462t

t = 2.996/0.0462

t = 64.848

Rounding this to the nearest tenth is 64.8 years

Hence, it will take the isotope 64.8 years to decay to 25 grams