Question

Of 122 adults selected randomly from one town, 27 of them smoke. The 99% confidence interval for the true percentage of all adults in the town that smoke is _____________.13.2% < p < 30.99%14.8< p < 29.5%15.9% < p < 28.3%18.4%< p < 25.9%

Answer 1

You know that of 122 adults selected randomly from one town, 27 of them smoke.

Then, you need to use this formula for Confidence Interval:

`CI=p\pm z_{(\alpha)/(2)}\sqrt[]{(p(1-p))/(n)}`

Where "p" is the proportion, "z" is the value of confidence level, and "n" is the number of elements in the sample.

You need to find the 99% confidence interval for the true percentage of all adults in the town that smoke.

By definition, the value of "z" for a 99% confidence interval is:

`z_{(\alpha)/(2)}=2.57583`

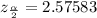
In this case:

`\begin{gathered} n=122 \\ \\ p=(27)/(122) \end{gathered}`

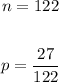
Therefore, substituting values into the formula and evaluating, you get:

`CI=(27)/(122)\pm(2.57583)_{}\sqrt[]{((27)/(122)(1-(27)/(122)))/(122)}`
`CI=(27)/(122)\pm(2.57583)_{}\sqrt[]{((27)/(122)(1-(27)/(122)))/(122)}`

You will two values:

`CI_1=(27)/(122)+(2.57583)_{}\sqrt[]{((27)/(122)(1-(27)/(122)))/(122)}\approx31\text{\%}`
`CI_2=(27)/(122)-(2.57583)_{}\sqrt[]{((27)/(122)(1-(27)/(122)))/(122)}\approx13\text{\%}`

Hence, the answer is: First option.