Solution:
Given:
A pair of linear equations
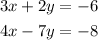
The solution to the system of equations is gotten by solving for the unknowns (x and y) simultaneously.
Solving for the solution using the elimination method,

Alternatively, solving the systems of equations using graphical method, the solution is seen at the point of intersection of the two lines as shown below;
Therefore, the solution to the system of equations as an ordered pair (x,y) is (-2,0).