Answer
The horizontal distance (x) when the ball hits the ground is 12.8 feet
SOLUTION
Problem Statement
The question tells us that a ball thrown from a height of 6 feet, is modeled by the following equation:

We are asked to find the horizontal distance covered by the ball before hitting the ground.
Method
- To find the horizontal distance covered before hitting the ground implies that the height of the ball after some horizontal distance covered must be zero.
- This is because for the ball to hit the ground, the height of the ball over the earth must be zero. This means that:
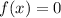
- Thus, to find the horizontal distance x when the ball hits the ground, then we need to equate the function of f(x) to zero and then solve for x.
That is:
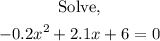
Implementation
![\begin{gathered} -0.2x^2+2.1x+6=0 \\ \text{ We can solve this using the Quadratic Formula:} \\ \\ \text{The Quadratic formula is defined below:} \\ \text{Given the following Quadratic Equation:} \\ ax^2+bx+c=0 \\ \\ \text{The Quadratic formula is:} \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \\ \text{From the equation given, we can see that:} \\ a=-0.2,b=2.1,c=6 \\ \\ \therefore x=\frac{-2.1\pm\sqrt[]{2.1^2-4(-0.2)(6)}}{2(-0.2)} \\ \\ x=(-2.1\pm3.0348)/(-0.4) \\ \\ x=(-2.1-3.0348)/(-0.4)\text{ or }(-2.1+3.0348)/(-0.4) \\ \\ \\ \therefore x=12.837\text{ or }-2.337. \\ \\ \text{ Since a horizontal distance cannot be negative, we have that:} \\ x=12.837\approx12.8\text{ (to the nearest tenth)} \end{gathered}]()
Final Answer
The horizontal distance (x) when the ball hits the ground is 12.8 feet