The vertices of the given quadrilateral GHJK are:
G = (3, 2)
H = (-3, 3)
J = (-5, -2)
K = (1, -3)
a) To find the length of JK and GH we will use the rule of the distance
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
For JK, let J = (x1, y1) and K = (x2, y2)
![\begin{gathered} JK=\sqrt[]{(1--5)^2+(-3--2)^2} \\ JK=\sqrt[]{(1+5)^2+(-3+2)^2} \\ JK=\sqrt[]{(6)^2+(-1)^2} \\ JK=\sqrt[]{36+1} \\ JK=\sqrt[]{37} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gj6uq23dkrjyxj1y9agv45k3u3vrs4w6yf.png)
For GH, let G = (x1, y1) and H = (x2, y2)
![\begin{gathered} GH=\sqrt[]{(-3-3)^2+(3-2)^2} \\ GH=\sqrt[]{(-6)^2+(1)^2} \\ GH=\sqrt[]{36+1} \\ GH=\sqrt[]{37} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5t49hcj0lakt1pqb0pgd01fyigo05o14so.png)
b) We will use the rule of the slope to find the slopes of JK and GH

For JK
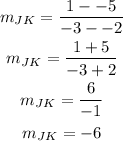
For GH
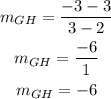
c) From parts a and b
JK = GH
JK // GH because they have the same slopes
Then GHJK is a parallelogram because it has a pair of opposite sides that are both congruent and parallel
The answer is A