Question

I need help with two multiple choice questions, algebra.questions number 5 and 6

Answer 1

In order to find the temperature, we must find the intensity of the light at the time we are evaluating.

Since the function is model since 6:00 am and we need the temperature at 2:00 pm we need to know how many hours have passed from 6:00 am to 2:00 pm.

This is 8 hours.

Then,

`t=8h`

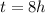
Now that we have the corresponding time we can find the intensity by replacing t for 8.

`\begin{gathered} I=(12h-h^2)/(36) \\ I=(12\cdot8-8^2)/(36) \\ I=(96-64)/(36) \\ I=(32)/(36) \\ I=(8)/(9) \end{gathered}`

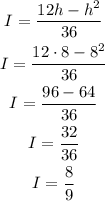
Continue by calculating the temperature using the function for the temperature with the intensity of the light calculated at 2:00 pm

`\begin{gathered} T=\sqrt[]{5000\cdot I} \\ T=\sqrt[]{5000\cdot(8)/(9)} \\ T=\sqrt[]{(40000)/(9)} \\ T=(200)/(3)\approx66.67\cong67 \end{gathered}`

The closest to the temperature is 67.