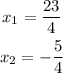When dealing with an absolute value, there are two cases that must be analyzed.
Case 1: 4x-9 > 0
Then:
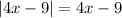
Solving the equation for x:
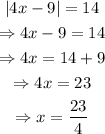
Case 2: 4x-9 < 0
Then:
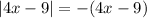
Soving the equation for x:
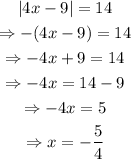
The graph of the function f(x)=|4x-9| is:
Therefore, the solution set is: