Question

A. Solve for c: E = mc2

Answer 1

Starting with the equation:

`E=mc^2`

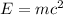
Divide both sides by m, provided that m is not equal to 0:

`\begin{gathered} (E)/(m)=(mc^2)/(m) \\ \Rightarrow \\ (E)/(m)=c^2 \end{gathered}`

Take the square root of both sides of the equation:

`\sqrt[]{(E)/(m)}=\sqrt[]{c^2}`

Remember that the square root of a squared number is equal to the absolute value of that number:

`\sqrt[]{(E)/(m)}=|c|`

This equation for c has two possibilities, whether c is positive or negative:

`c=\pm\sqrt[]{(E)/(m)}`

In the context of physics, only the positive value has a physical meaning.