For part A, first observe that the line in the graph is not dotted, but continuous, so you have an inequality of type ≤ or ≥.
Now, notice that if you take some random points on the Cartesian plane, for example, (5,6), (4,-3),(-3,6) and (-6,-7) the first and third points belong to the shaded region, while the second and fourth points do not.
As you can see in the points that if they belong to the shaded region, the y coordinate is greater than the x coordinate.
On the other hand, at the points that do not belong to the shaded region, the Y coordinate is less than the x coordinate.
Therefore, the inequality represented by the graph is
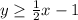
For part B, you can take, for example, the points or ordered pairs that you used in part A and replace in the inequality. So for (5,6) you have
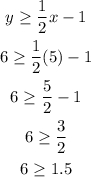
Since you get a true statement then the point (5,6) is a solution. Now for (-3,6) you have
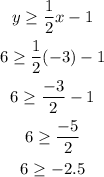
Since you get a true statement then the point (-3,6) is a solution too.
Therefore, two solutions to the graph are (5,6) and (-3,6).