ANSWER :
a. 1/3
b. 0
EXPLANATION :
From the problem, we have the function :

Factor the numerator and the denominator :
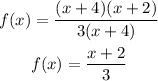
a. Getting the first derivative :
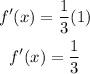
So what ever the value of x, the derivative is always 1/3
The answer is 1/3
b. f''(5), the derivative of any constant is always 0.
Since the first derivative is a constant, therefore, the second derivative is 0.