The absolute value is defined as two cases, if we substitute what we have in this example
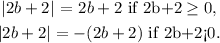
Then, if we substitute this equations
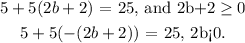
The first part becomes in
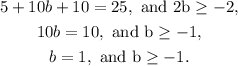
Then, one solution is b=1 since both conditions are fulfilled.
From the second part we have
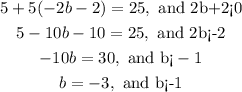
Thus, the other soultion is b=-3 since it satisfies both conditions.