First, we find angle K
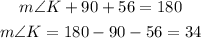
Then, we use the inscribed angle theorem
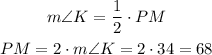
Hence, the arc PM measures 68°.
Also, the arc MP measures 68° because it's the same arc.
If arc MT is 170°, and MP is 68°, then
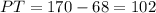
Then, we observe that arc KTP is equal to 180° because it's half the circumference. So,
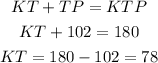
Hence, arc KT measures 78°.