Question

A helium balloon has a volume of 8.89 liters, or 0.00889 cubic meters. Air has a density of 1.29 kilograms per cubic meter, and helium has a density of 0.177 kilograms per cubic meter.a. What is the weight of the helium inside the balloon?b. What is the buoyant force exerted on the balloon?c. What is the net force on the balloon? Neglect the weight of the rubbery material that comprises the actual balloon. . How many identical balloons would be needed to lift a child of mass 24.9 kilograms?

Answer 1

Given:

The volume of a helium balloon: 8.89 liters or 0.00889 cubic meters

The density of helium: 0.177 kilograms per cubic meters

The density of the air: 1.29 kilograms per cubic meters

To find:

a) weight of the helium inside the balloon.

b) the buoyant force exerted on the balloon.

c) the net force on the balloon.

d) number of identical balloons needed to lift a child of mass 24.9 kilograms.

Step-by-step explanation:

a)

The expression for the density of the balloon is:

`Density\text{ of helium=}\frac{Mass\text{ of helium}}{Volume\text{ of helium}}`

Rearrange the above expression to find the mass of the helium.

`Mass\text{ of helium=Density of helium}* Volume\text{ of helium}`

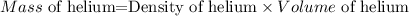
Substitute the values from the given data, we get:

`\begin{gathered} Mass\text{ of helium=0.177}(kg)/(m^3)*0.00889\text{ m}^3 \\ Mass\text{ of helium=0.001573 kg} \end{gathered}`

Thus, the mass of the helium is 0.001573 kg.

The weight of an object is the product of its mass and gravitational acceleration. Thus, the weight of helium is

`\begin{gathered} Weight\text{ of helium=mass of helium}* g \\ \end{gathered}`

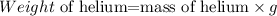
here, g is the acceleration due to gravity.

Substitute the values, and we get:

`\begin{gathered} Weight\text{ of helium=0.001573 kg }*9.8\text{ }(m)/(s^2) \\ Weight\text{ of helium=0.01542 N} \end{gathered}`

The weight of helium is 0.001542 Newtons.

b)

The expression for buoyant force is:

`F=\rho gV`

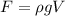
here, ρ is the density, g is the acceleration due to gravity and V is the volume.

To find the buoyant force exerted by helium on the balloon, substitute the values for helium in the above equation.

`\begin{gathered} F=0.177\text{ }(kg)/(m^3)*9.8\text{ }(m)/(s^2)*0.00889\text{ m}^3 \\ F=0.01542\text{ }(kg\cdot m)/(s^2) \\ F=0.01542\text{ N} \end{gathered}`

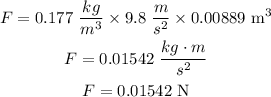
The buoyant force exerted on the baloon is 0.01542 Newtons.

c)

The buoyant force exerted by the balloon is 0.01542 N and it acts in an upward direction. Whereas, the other force acting on the balloon is the force due to gravity, the weight of the balloon. The weight of the balloon is 0.01542 N and is always acts in the downwards direction.

Since the magnitude of buoyant force exerted on a balloon is equal to the weight of the balloon. Both these forces are acting in opposite directions. Thus the net effect will be zero.

`\begin{gathered} F_(net)=F-W \\ F_(net)=0.01542\text{ N -0.01542 N} \\ F_(net)=0\text{ N} \end{gathered}`

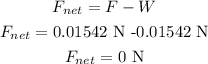
Thus, the net force acting on the balloon is 0 Newtons.

d)

For a helium balloon, 1 liter of helium can lift 1 gram of mass.

The mass of the child is 24.9 kg = 24900 grams.

Thus, to lift a child of mass 24900 grams, 24900 liters of helium is required.

Now, one balloon contains 8.89 liters of helium, thus for 24900 liters of helium volume, the number of ballons required will be,

`\frac{1\text{ balloon}}{n\text{ balloons}}=\frac{8.89\text{ liters}}{24900\text{ liters}}`

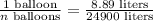
Rearranging above equation to find n, we get

`\begin{gathered} n\text{ balloons = }(24900)/(8.89) \\ n\text{ balloons = 2800.89} \end{gathered}`

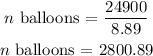
Thus, approximately 2801 helium balloons are required to lift a child of mass 24.9 kg.

Final answer:

a) The weight of helium is 0.001542 Newtons.

b) The weight of helium is 0.001542 Newtons.

c) The net force acting on the balloon is 0 Newtons.

d) Approximately 2801 helium balloons are required to lift a child of mass 24.9 kg.