Question

a motor take 5 hours to travel 100 miles going upstream. the return trip takes 2 hours going downstream. what is the rate of the boat in still water and what is the rate of the current?

Answer 1

Step 1. The information we have is:

It takes the boat a time of 5 hours to go 100 miles upstream, and 2 hours to return going downstream.

Required: Find the velocity or rate of the boat, and the velocity or rate of the current.

Step 2. Remember the formula for velocity:

`v=(d)/(t)`

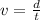
where v is the velocity or rate, d is the distance and t is time.

Step 3. Let Vb be the rate of the boat, and Vc be the rate of the current. When the boat is going upstream, the rate of the current is subtracted from the rate of the boat. The distance d is 100 miles, and the time t is 5 hours.

Using the velocity or rate formula:

`\begin{gathered} v=(d)/(t) \\ \downarrow\downarrow \\ V_b-V_c=(100)/(5) \end{gathered}`

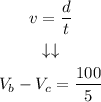
SImplifying:

`V_b-V_c=20`

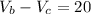
This will be our first equation.

Step 4. When the boat is going downstream, the rate of the current is added to the rate of the boat. The distance is again 100 miles, but this time the time is 2 hours.

Using the velocity or rate formula:

`\begin{gathered} v=(d)/(t) \\ \downarrow\downarrow \\ V_b+V_c=(100)/(2) \end{gathered}`

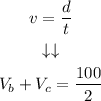
Simplifying:

`V_b+V_c=50`

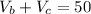
This will be our second equation.

Step 5. Summary of our two equations:

`\begin{gathered} V_b-V_c=20 \\ V_b+V_c=50 \end{gathered}`

Step 6. Solve the system of equations to find the two rates.

To solve the system of equations we will use the elimination method. This method consists of adding the equations to eliminate one variable. In this case, we will add the two equations from step 5 to eliminate Vc:

The result is the equation:

`2V_b=70`

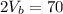
Solving for Vb:

`\begin{gathered} V_b=(70)/(2) \\ \boxed{V_b=35} \end{gathered}`

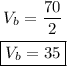
Step 7. Once we know the value of Vb, substitute it on the second equation from step 5 to find Vc:

`\begin{gathered} V_b+V_c=50 \\ \downarrow\downarrow \\ 35+V_c=50 \\ \text{Solving for Vc:} \\ V_c=50-35 \\ \boxed{V_c=15} \end{gathered}`

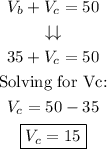
Both rates are in miles per hour.

Answer:

`\begin{gathered} \text{Rate of the boat in still water: 35 mi/h} \\ \text{Rate of the current: 15 mi/h} \end{gathered}`