Question

3.17Using substitution, identify the ordered pair that is an element of the solution set of thesystem of equations.3x + y = 2y-x= -6

Answer 1

Hello

To solve this question, we are asked to use substitution method.

The given equation is

`\begin{gathered} 3x+y=2\ldots\text{equ(i)} \\ y-x=-6\ldots\text{equ(}ii) \end{gathered}`

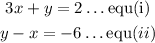
From equation (ii), let's make y the subject of formula

`\begin{gathered} y-x=-6 \\ y=x-6\ldots\text{equ(}iii) \end{gathered}`

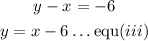
Put equation (iii) into equation (i)

`\begin{gathered} 3x+y=2 \\ y=x-6 \\ 3x+(x-6)=2 \\ 3x+x-6=2 \\ \text{collect like terms} \\ 4x=2+6 \\ 4x=8 \\ \text{divide both sides by the coefficient of x} \\ (4x)/(4)=(8)/(4) \\ x=2 \end{gathered}`

We have the value of one of the ordered pair and we can use it to find the other one.

Put x = 2 in either equation (i) or (ii)

Using equation (ii)

`\begin{gathered} y-x=-6 \\ x=2 \\ y-(2)=-6 \\ \text{collect like terms} \\ y=-6+2 \\ y=-4 \end{gathered}`

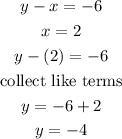
The value of x and y is (2, -4) and the ordered pair can be written as (2, -4)