The exam has 4 true or false questions.
For each question, if you select the answer at random, the probability of answering true or falce are equal.
P(T)=P(F)=1/2
Three of the four answers are "False"
You have the following posibilities:
"1st answer is False" and "2nd is False" and "3rd is False" and "4rt is True"
or
"1st answer is False" and "2nd is False" and "3rd is True" and "4rt is False"
or
"1st answer is False" and "2nd is True" and "3rd is False" and "4rt is False"
or
"1st answer is True" and "2nd is False" and "3rd is False" and "4rt is False"
You can symbolize this as:
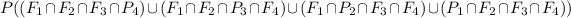
Since the probability if False is equal for all questions, and the terms in all 4 posibilities are equal you can simplify that expression to
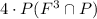

The probability of 3 out of the 4 answers being False is 1/4