ANSWER:
250 J
Explanation:
F = 20N is required to stretch the spring by 4 meters
We know that the force is equal to:
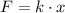
We solve for k (spring constant):
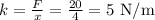
The work done in stretching the spring is given by the following equation (in this case the stretch is 10 meters:
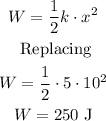
The work required is 250 joules.