c)rhombus
Step-by-step explanationthe slope of a line or segment is given by:
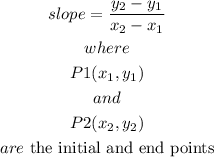
so
Step 1
find the slope of the given segments
a)slope of TU
let
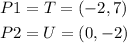
now, replace in the expression
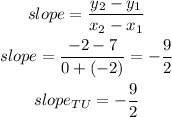
b) Slope of UV
Let
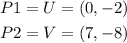
now, replace in the expression
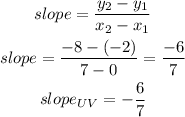
c)slope of VW
Let
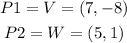
now, replace in the expression
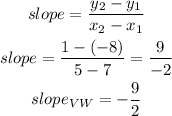
d) slope of WT
let
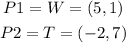
now, replace in the expression
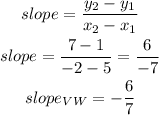
therefore, for the slopes the answer is
Step 2
lengths
the distance(d) between 2 points(P1 and P2) is given by:
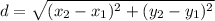
so
a) length of TU
let
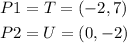
replace:
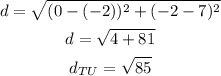
b) length UV
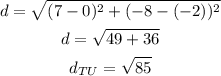
c)Length VW
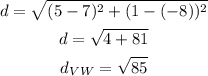
d)length WT
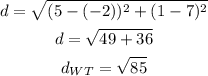
so
Step 3
finally, we have a parallelogram where all sides are equal, this is called
rhombus
I hope this helps you