The form of the equation of the circle is
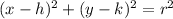
Where (h, k) are the coordinates of the center
r is the radius
Since the endpoints of the diameter are (11, 2) and (-7, -4), then
The center of the circle is the midpoint of the diameter
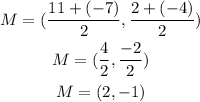
The center of the circle is (2, -1), then
h = 2 and k = -1
Now we need to find the length of the radius, then
We will use the rule of the distance between the center (2, -1) and one of the endpoints of the diameter we will take (11, 2)
![\begin{gathered} r=\sqrt[]{(11-2)^2+(2--1)^2} \\ r=\sqrt[]{9^2+3}^2 \\ r=\sqrt[]{81+9} \\ r=\sqrt[]{90} \\ r^2=90 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ksgy7uzp86k75xxruwxl6opg55ky7vw9jl.png)
Now substitute them in the rule above
![undefined]()