Question

5. Noah orders an extra-large pizza. It costs $12.49 for the pizza plus $1.50for each topping. He orders an extra-large pizza with t toppings that costsa total of d dollars. Select ALL of the equations that represent therelationship between the number of toppings t and total cost d of the pizzawith t toppings."12.49 + t = 012.49 + 1.501 - 012.49 +1.500 t12.49 = d + 1.500t = (d. 12.49) / 1.5t=d12.49/1.5

Answer 1

The cost of 12.49 is fixed, while the extra cost for toppings is 1.5 per topping.

If we have a total of t topping, the cost of the toppings will by 1.50t, adding the fixed cost, we will have the total cost, which should be equal to d. so we have the equation:

`d=12.49+1.50t`

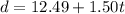
Now, we can manipulate the equation to check which ones are equivalent to it.

As we can see, the first one is missing the 1.50, so it is not equivalent.

The second have the 1.50, it is just inverted:

`12.49+1.50t=d`

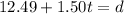
So, it is equivalent.

The third had the t and d switched, so it is not equivalent.

The fourth get the 1.50t to the other side, but don't change the sign accordingly, so it is not equivalent.

The fifth solved for t let's do that:

`\begin{gathered} 12.49+1.50t=d \\ 1.5t=d-12.49 \\ t=((d-12.49))/(1.5) \end{gathered}`

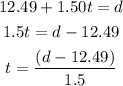
So, it is equivalent.

The sixth don;t distribute the denominator correctly, so it is not equivalent.

So, the alternatives that are equivalent are:

`\begin{gathered} 12.49+1.50t=d \\ t=(d-12.49)/1.5 \end{gathered}`

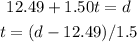
The second and fifth.