Question

(c) How far from the thrower does the ball hit the ground?

Answer 1

Given equation of the parabola is,

`h(x)=-(1)/(20)x^2+8x+6`

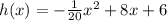
where h(x) is the height function and x denotes the horizontal distance.

To find the distance thrown does the ball hit the ground.

we get that,

`\begin{gathered} h(x)=0 \\ -(1)/(20)x^2+8x+6=0 \end{gathered}`

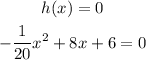
To find the value of x, we get

`-(1)/(20)x^2+8x+6=0`

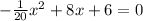
In order to cancel the denominater multiply by -20, we get

`x^2-160x-120=0`

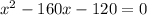
Factorise the above equation, we get

`x=\frac{160\pm\sqrt[]{(160)^2+4(120)}}{2}`
`x=\frac{160\pm\sqrt[]{4(6400)+4(120)}}{2}`
`x=\frac{160\pm2\sqrt[]{6400+120}}{2}`
`x=80\pm\sqrt[]{6520}`
`x=80\pm2\sqrt[]{1630}`

The distance between the initial and final point is,

`d=\lvert80-2\sqrt[]{1630}-(80+2\sqrt[]{1630})\rvert`
`d=4\sqrt[]{1630}`

Answer is:

`d=4\sqrt[]{1630}\approx161.49`