1) Given y = x+2 and y = -4x-8.
Since the left hand sides of both equations are same, equate the right hand side of both the equations.
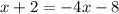
Add 4x on both sides.
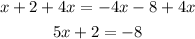
Add -2 on both sides.
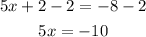
Divide by 5 on both sides.
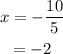
Substitute the value of x into y = x+2.
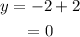
Solution is (-2,0).
2) Given y = 3x+1 and y = -2x+6.
Since the left hand sides of both equations are same, equate the right hand side of both the equations.
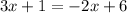
Add 2x on both sides.
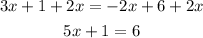
Add -1 on both sides.
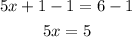
Divide by 5 on both sides.
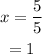
Substitute the value of x into y = 3x+1.
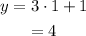
Solution is (1, 4).
3) Given y = -3x-6 and 6x+2y = -2.
Substitute -3x-6 for y into 6x+2y = -2.
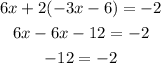
which is not possible. Hence the given system of equations has no solution.
4) Given y = -5 and -8x+4=-20.
From the second equation, -8x+4 = -20, solve for x.
Add -4 on both sides.
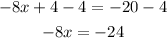
Divide by -8 on both sides.
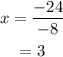
Solution is (-5, 3).