Question

x=0,0.5,1,3,3.5,4,5y= 63,72,75,81,84,90,93calculate the correlation coefficient, r.round answer to the 3 decimal places

Answer 1

In order to find the correlation coefficient r, we can use the formula:

`r=\frac{7\sum ^{}_{}(xy)-\sum ^{}_{}x\sum ^{}_{}y}{\sqrt[]{\lbrack7\sum ^{}_{}x^2-(\sum ^{}_{}x)^2\rbrack\cdot\lbrack7\sum ^{}_{}y^2-(\sum ^{}_{}y)^2\rbrack}}`

where the sum must be taken upon all 7 values of x and y.

So, let's find each term and then use them in the formula:

`\begin{gathered} 7\sum ^{}_{}(xy)=7(0\cdot63+0.5\cdot72+1\cdot75+3\cdot81+3.5\cdot84+4\cdot90+5\cdot93) \\ =7\cdot1473=10311 \end{gathered}`
`\begin{gathered} \sum ^{}_{}x\sum ^{}_{}y=(0+0.5+1+3+3.5+4+5)\cdot(63+72+75+81+84+90+93) \\ =17\cdot558=9486 \end{gathered}`
`\begin{gathered} 7\sum ^{}_{}x^2-(\sum ^{}_{}x)^2 \\ 7\cdot(0^{2^{}}+0.5^2+1^2+3^2+3.5^2+4^2+5^2)-(0+0.5+1+3+3.5+4+5)^2 \\ 7\cdot63.5-17^2 \\ 444.5-289 \\ 155.5 \end{gathered}`
`\begin{gathered} 7\sum ^{}_{}y^2-(\sum ^{}_{}y)^2 \\ 7\cdot(63^2+72^2+75^2+81^2+84^2+90^2+93^2)-(63+72+75+81+84+90+93)^2 \\ 7\cdot45144-558^2 \\ 316008-311364 \\ 4644 \end{gathered}`

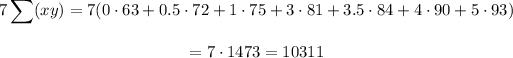
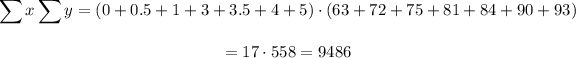
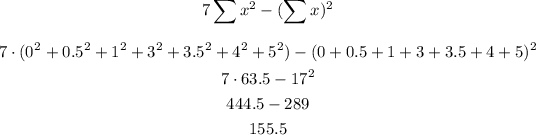
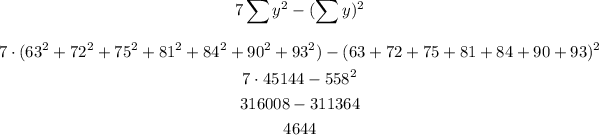
Now, we need to use them in the formula to find r:

`r=\frac{10311-9486}{\sqrt[]{155.5\cdot4644}}=\frac{825}{\sqrt[]{722142}}\cong0.9708`

Finally, round the answer to the 3 decimal places, we find

r = 0.971