Question

use the distribution method to solve the system of equations. enter your answer as an ordered pair. y=7x+6 and y=x+20

Answer 1

y = 7x+6

y = x + 20

Substituting the value of y of the second equation into the first equation, we get:

x + 20 = 7x + 6

20 - 6 = 7x - x

14 = 6x

14/6 = x

7/3 = x

Replacing this value into the first equation, we get:

`\begin{gathered} y=7\cdot(7)/(3)+6 \\ y=(49)/(3)+6 \\ y=(49+6\cdot3)/(3) \\ y=(67)/(3) \end{gathered}`

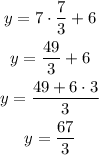
The solution as an ordered pair is (7/3, 67/3)