Question

What is the slope of a line perpendicular to the line whose equation is x+3y=-15. Fully simplify your answer.

Answer 1

The slope of the line perpendicular line of the equation is 3

Explanation:

What to find? The slope of a line perpendicular to the line whose equation is x + 3y = -15

Given the equation

x + 3y = -15

The slope-intercept form of an equation is given as

`y\text{ = mx + b}`

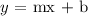
Where m = slope of the line

y = the intercept of the y-axis

The next step is to re-arrange the above equation in the slope-intercept format

`\begin{gathered} \text{Given the equation of a straight line as} \\ x\text{ + 3y = -15} \\ \text{Isolate 3y by substracting x from both sides} \\ x\text{ - x + 3y = -15 - x} \\ 3y\text{ = -x - 15} \\ \text{Divide through by 3} \\ (3y)/(3)\text{ = }(-1)/(3)x\text{ -}(15)/(3) \\ y\text{ = }(-1)/(3)x\text{ - 5} \\ \text{Hence, the slope}-\text{intercept form of the above equation is given as} \\ y\text{ = }(-1)/(3)x\text{ - 5} \end{gathered}`

NB: That the two lines are perpendicular to each other

From y = mx + b

m = -1/3

The slope of the equation

`\begin{gathered} \text{ For two perpendicular lines, we can calculate the slope as follows} \\ m_1\cdot m_2\text{ =- 1} \\ \text{where m}_1\text{ = }(-1)/(3) \\ (-1)/(3)\cdot m_2\text{ = -1} \\ (-1\cdot m_2)/(3)=\text{ -1} \\ \text{Cross multiply} \\ -m_2\text{ = -1 }\cdot\text{ 3} \\ -m_2\text{ = -3} \\ \text{Divide through by -1} \\ (-m_2)/(-1)\text{ = }(-3)/(-1) \\ m_2\text{ = }3 \\ \text{Hence, the slope of the perpendicular line to the equation is 3} \end{gathered}`