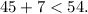Question

A Is it possible to construct a triangle with lengths of 7, 54, and 45? EXPLAIN why or why not?

Answer 1

For a, b, and c to be the lengths of a triangle they must satisfy the following system of inequalities:

`\begin{gathered} a+b>c, \\ a+c>b, \\ b+c>a\text{.} \end{gathered}`

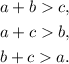
Now, notice that:

`\begin{gathered} 7+54>45, \\ 45+54>7,\text{ } \\ 45+7=52<54. \end{gathered}`

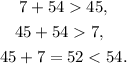
Since the given numbers do not satisfy the last inequality, then they cannot be the lengths of a triangle.

Answer: No it is not possible to construct a triangle with lengths 7, 54 and 45, because:

`45+7<54.`