Question

A right triangle has an area of 54 ft2 and a hypotenuse of 25 ft long. What are the lengths of its other two sides?

Answer 1

By theorem we have the following:

`h^2=a^2+b^2`

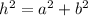
And, we are given:

`A=(a\cdot b)/(2)\Rightarrow2A=a\cdot b`

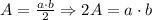
Then:

`\Rightarrow4A^2=a^2b^2\Rightarrow4A^2=a^2(h^2-a^2)`
`\Rightarrow a^4-h^2a^2+4A^2=0`

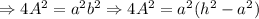
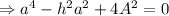
Now, we replace h and A:

`a^4-(25)^2a^2+4(54)^2=0`

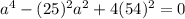
And solve for a:

`a^4-625a^2+11664=0`

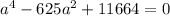
Then, the possible values for a are:

`a=\begin{cases}a_1=-(29)/(2)-\frac{\sqrt[]{409}}{2} \\ a_2=(29)/(2)-\frac{\sqrt[]{409}}{2} \\ a_3=\frac{\sqrt[]{409}}{2}-(29)/(2) \\ a_4=(29)/(2)+\frac{\sqrt[]{409}}{2} \\ \end{cases}`

We can see that a1, and a2 are not solutions, therefore a2 and a4 are.

So, the two possible b sides are then:

`b_2=\sqrt[]{25^2-((29)/(2)-\frac{\sqrt[]{409}}{2})^2}\Rightarrow b_2\approx24.99`

and:

`b_4=\sqrt[^{}]{25^2-((29)/(2)+\frac{\sqrt[]{409}}{2})^2}\Rightarrow b_(4\approx)15.50`

So, the lengths of the two sides can be:

a = 4.38 and b = 24.99

or

a = 24.61 and b = 15.50