ANSWER and EXPLANATION
A centripetal force is a force acting on an object that keeps it moving in a circular path.
Gravitational force is an attractive force acting between two objects.
Gravitational force can only be equal to centripetal force when the gravitational force (attractive force) is the only force keeping that object moving in a circular path. In this case, we can say that the gravitational force is the centripetal force keeping the object in orbit.
Mathematically, we can write that:
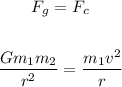
where G = gravitational constant
m1, m2 = masses of the two objects
r = distance between the objects
v = velocity of the object in consideration