The unit rate represented in the equation y = 3/5x is the value multiplying x, that is, the unit rate is 3/5.
In order to find the unit rate of each table, we just need to divide the y-values by the x-values.
So, the unit rate of the first table is:
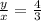
The value 4/3 is greater than the value 3/5.
In the second table we have that:
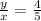
The value 4/5 is greater than the value 3/5;
In the third table, we have that:
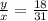
In order to compare this fraction with 3/5, we need to make them be in the same denominator, so we have to calculate the least common multiple of the denominators.
Since 5 and 31 are prime numbers, the LCM is the product of both numbers.
So we have that:
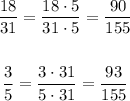
The number 90/155 is lesser than 93/155, therefore 18/31 is lesser than 3/5, so the answer is the third table.