The cross section of the canal will form a trapezoid. First, find the area of the cross section. The area of a trapezoid is defined as

Substitute the following values and we get the area
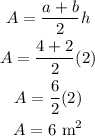
Now that we have the area of the cross section, multiply it to the length of the irrigation canal.
![\begin{gathered} \text{Before multiplying, all units must be the same, convert km to meters} \\ 10\operatorname{km}\rightarrow10,000\text{ meters} \\ 6\text{ m}^2*10000\text{ meters} \\ \Longrightarrow60000\text{ m}^3 \end{gathered}]()
Therefore, they have to excavate 60,000 cubic meters of earth to make the canal.