Question

Liz's math test included a survey question asking how many hours students spent studying for the test. Thescatter plot below shows the relationship between how many hours students spent studying and their score onthe test. A line was fit to the data to model the relationship.Which of these linear equations best describes the given model?A) ŷ = 10x + 20B) ŷ = 20x + 20Or C) ŷ = -20x + 20Based on this equation, estimate the score for a student that spent 3.8 hours studying.Round your answer to the nearest hundredth.__________.

Answer 1

Answer: B. y = 20x +20

The score for a student that spent 3.8 hours studying is expected to be 96.

Step by step solution:

The point-slope form of a linear equation is y = mx + b, where m is the slope and b the intercept with the y-axis.

To find the line that fits the data and model the relationship, we need to find the slope. Let

y = Test score

x = Study time (hours)

`\begin{gathered} m=(y_1-y_2)/(x_1-x_2) \\ (x_1,y_1_{})\text{ and }(x_2,y_2)\text{ Point in the line} \end{gathered}`

Two pair of coordinates from the line are (2, 60) and (3, 80):

`m=(60-80)/(2-3)=(-20)/(-1)=20`

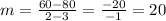
We have m = 20, and b = 20 (intercept with the y-axis)

The equation that model the relationship is:

`y=20x+20`

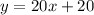
Second Part. Basing ourselves on the above equation, estimate the score for a student that spent 3.8 hours studying x = 3.8.

`\begin{gathered} y=(20\cdot3.8)+20 \\ y=76+20 \\ y=96 \end{gathered}`

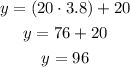
The score for a student that spent 3.8 hours studying is expected to be 96.