Question

Only about 16% of all people can wiggle their ears. Is this percent different for millionaires? Of the 342 millionaires surveyed, 58 could wiggle their ears. What can be concluded at the α = 0.01 level of significance?For this study, we should use Select an answerThe null and alternative hypotheses would be: H0: ? Select an answer (please enter a decimal) H1: ? Select an answer (Please enter a decimal)The test statistic ? = (please show your answer to 3 decimal places.)The p-value = (Please show your answer to 3 decimal places.)The p-value is ? α Based on this, we should Select an answer the null hypothesis.Thus, the final conclusion is that ...The data suggest the population proportion is not significantly different from 16% at α = 0.01, so there is statistically insignificant evidence to conclude that the population proportion of millionaires who can wiggle their ears is different from 16%.The data suggest the populaton proportion is significantly different from 16% at α = 0.01, so there is statistically significant evidence to conclude that the population proportion of millionaires who can wiggle their ears is different from 16%.The data suggest the population proportion is not significantly different from 16% at α = 0.01, so there is statistically significant evidence to conclude that the population proportion of millionaires who can wiggle their ears is equal to 16%.Part a options:- a. t- test for a population mean- z-test for a population proportionPart b options:(left box): u; ?; p(right box): >; =; =/; >Part c options:t; zPart e options:<; >Part f options:ACCEPT, REJECT, FAIL

Answer 1

Part a:

In this study, we have only a reference value of 16% (the proportion of people that can wiggle ears) and a population of 342 millionaires whose results we want to compare with this reference value. Since there is a relativelly high number of millionaries that were surveyed, we should use the z-test for a population proportion.

Part b:

It p is the sample proportion, the null hypothesis, in this case, is given by:

`H_0:p=0.16`

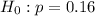
Therefore, the alternative hypothesis is given by:

`H_1:p\\e0.16`

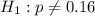
Part c:

According to the data, the z-score is given by:

`z=\frac{(58)/(342)-\cdot0.16}{\sqrt{(1)/(342)\cdot(58)/(342)(1-(58)/(342))}}\approx0.473`

Part d:

According to the normal table, the p-value related to z-score given by:

0.638

Part e:

Therefore, we can check that this p-value is > a

Part f:

Based on this, we should ACCEPT the null hypothesis.

Part g:

Thus, the final conclusion is that the data suggest the population proportion is not significantly different from 16% at a = 0.01, so there is statistially significant evidence to conclude that the population proportion of millionaries who can wiggle their ears is equal to 16%.