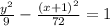Given the Foci of the hyperbola:
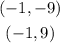
And the Vertices:
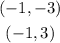
You can plot the Foci on a Coordinate Plane:
Notice that the blue line represents the Vertical Transverse Axis. Then, the equation has this form:
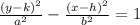
You need to find the Center using the Midpoint Formula, in order to find the Midpoint between the Foci and the Midpoint between the vertices:
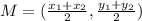
- For the Foci:
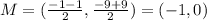
- For the Vertices:
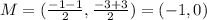
Therefore:
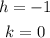
Now you need to find "a". This is the distance from the center to the vertices:
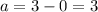
Find "b" with this formula:
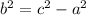
Knowing that "c" is the distance from the Foci to the center:
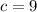
You get:
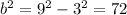
Therefore, you can write this equation:
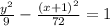
Hence, the answer is: