Answer
Event 3, Event 2, Event 4, Event 1.
Step-by-step explanation
Given data:
Box A has 6 purple pens and 2 blue pens.
Box B has 12 purple pens and 8 blue pens.
Let X represents purple, Y represents blue, and Z represents red.
Box A: n(X) = 6, n(Y) = 2, and n(Z) = 0. Hence, n(S) = 6 + 2 + 0 = 8
Box B: n(X) = 12, n(Y) = 8, and n(Z) = 0. Hence, n(S) = 12 + 8 + 0 = 20
So if a pen is randomly chosen from each box, the probability of:
Event 1: choosing a purple or blue pen from Box B. will be:
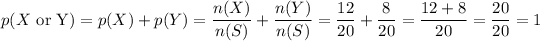
Event 2: choosing a blue pen from Box B will be:

Event 3: choosing a red pen from Box A will be:
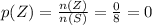
Event 4: choosing a purple pen from Box A wil be:
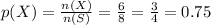
If a pen is randomly chosen from each box, the list of the events from least likely to most likely are:
Event 3, Event 2, Event 4, Event 1.