Question

2. The admission fee at a small fair is $2.50 for children and $4.00 for adults. On a certain day, 2400 people enter the fair and $7140 is collected. How many children and how many adults attended?

Answer 1

Given:

a.) The admission fee at a small fair is $2.50 for children and $4.00 for adults.

b.) On a certain day, 2400 people enter the fair and $7140 is collected.

Let,

x = total number of children

y = total number of adults

Let's generate two equations based on the given scenario:

EQUATION 1: Total number of children and adults entered the fair.

`\text{ x + y = }2400`

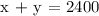
EQUATION 2: Total money collected from the admission.

`\text{ 2.5x + 4y = }$7140$`

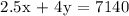
We will be using the substitution method. We get,

`\text{ x + y = }2400`
`\text{ y = }2400\text{ - x}`

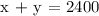
Substitute to Equation 2:

`\text{ 2.5x + 4y = }$7140$`
`\text{ 2.5x + 4(}2400\text{ - x) = }$7140$`
`\text{ 2.5x + 9600 - 4x = }$7140$`
`\text{ 2.5x - 4x = }$7140$\text{ - 9600 }`
`\text{ -1.5x }=\text{ }-2,460`
`\text{ }\frac{\text{-1.5x}}{-1.5}\text{ }=\text{ }(-2,460)/(-1.5)`
`\text{ x }=\text{ }1,640\text{ children}`

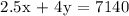
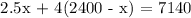
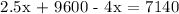
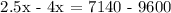
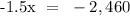
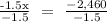
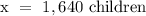
Therefore, 1,640 children went to the fair.

For the adults,

x + y = 2400

1,640 + y = 2400

y = 2400 - 1,640

y = 760 adults

In summary: 1,640 children and 760 adults went to the fair.