,By following these steps, we can find the value of this expression:
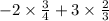
first we multiply both -2 and 3 by their corresponding fractions, we do this by just multiplying the numbers with the numerator of the fraction, like this:
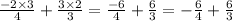
Now simplify the fractions:
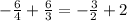
To sum fractions, we have to make sure that the denominators are the same, this is not the case, we can make their denominators the same by dividing and multiplying the two by two, like this:
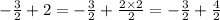
Now, we just have to sum up the numerators, like this:
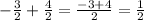
Then, the value of this expression is:
